While the original environment that the code was designed for Pendulum-v1 had a solve and termination case (950 steps in a close vertical position would win the environment and 20 degrees off top dead center would terminate the episode), the new environment had neither. It was easy for me to let the code run for 30 minutes with little signs of progress.

Environment Stats:

Description: Try to keep a frictionless pendulum standing up.

Action (Joint Effort) Min: -2.0 Max: 2.0

Reward: -(theta^2 + 0.1*theta_dt^2 + 0.001*action^2) Theta is normalized between -pi and pi. Therefore, the lowest cost is -(pi^2 + 0.1*8^2 + 0.001*2^2) = -16.2736044, and the highest cost is 0. In essence, the goal is to remain at zero angle (vertical), with the least rotational velocity, and the least effort.

Start State: Random angle from -pi to pi, and random velocity between -1 and 1

Stop State: None

Solve State: None

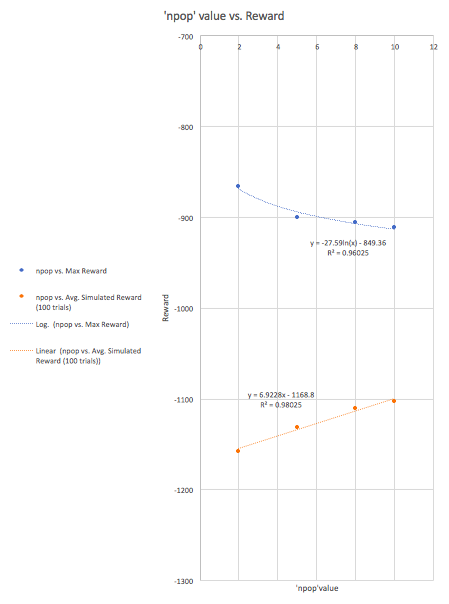
As a result, I felt I had to manually add to the code a ‘solve case’, which I placed at a reward of greater than -1000. Since the code began with a reward of ~-1700, I assumed that this would be a good benchmark for reinforcing the progress of the code.

Ultimately, I was interested most by changes in npop. To extend the metaphor associated with Evolutionary Strategies, npop is the number of version of a species that is being evaluated. This species is constituted by a certain set of parameters. Evolutionary Strategies takes a random seed and applies to it a randomizer operation. Each member of the species is tweaked by a certain amount (sigma value multiplied by this random number). Additionally, the number of episodes that the code is run is the product of npop and for-loop range. By decreasing the npop number, the number of episodes also goes down. Interestingly, though, is how the max reward can spike significantly toward the positive direction as the diversity of unique species can spike.

- The first figure shows the reward statistics for the original, unaltered code to set a baseline for comparison.
- The next table shows how changing sigma, alpha, npop, and for-loop range resulted in different rewards. - Despite interesting results from changing the learning rate (alpha), I was most interested by changes to npop, and felt I understood most the implications of changes to this value toward the output rewards. -The final figure shows that, interestingly, as npop increases, the max reward dips. I modeled this dip by a logarithmic function, as it seems asymptotic towards a reward of just over -920. This suggests that lower npop values may actually lend themselves to more volatile parameter changes, resulting in higher max rewards over a large episode ranges. -Before this relationship is well established, though, note that as these parameters are simulated for 100 trials, the average reward doesn't maintain at the purported maxes. Despite low npop values showing high rewards, the graph also shows that when these parameter values are put to the test for 100 trials, rewards are not necessarily sustainable.

Given more time with the code, the immediate next steps would be to explore other avenues of optimization. Through some research, I found several other articles which, along with the original paper, found that parallelization of the code was trivial (Evolutionary Strategies: Almost Embarassingly Parallel Optimization). Implementing Parallelization (pseudocode here:) could present opportunity for reducing run time and computation required tremendously. Further investigation towards the advantages of other input values (such as learning rate) could also present alternative frontiers for improvement.